近日,西南交通大学数学学院2021级数学基地班学生黄嘉驹的最新研究成果‘Iteration of a class of multi-plateau mappings’被sci期刊《Aequationes mathematicae》接收。黄嘉驹为该论文第一作者,合作者包括西南交通大学数学学院的刘鎏副教授与四川大学数学学院的张佳玲博士。期刊《Aequationes mathematicae》首次出版于1968年,专注于纯数学和应用数学,强调函数方程、动力系统、迭代理论、组合数学和几何等领域。目前该期刊为中科院三区期刊。
迭代是函数的自复合,是对运算的一种重复。许多物理,力学,生物学以及天文学问题的数学模型都是由迭代所描述。例如生活中银行借贷利率的计算过程就是迭代。在数学中,一切递推关系,例如等差数列,等比数列,证明微分方程解存在唯一性的Picard逼近都是一个迭代过程。在计算机科学中,也常常用数值方法把微分方程化为迭代以便于设计程序。迭代是非常重要的运算,它不仅为动态插值提供技术,还可用于信息加密。因此研究迭代具有十分重要的意义。
迭代的非线性特性在研究中带来了巨大挑战,并导致了许多复杂行为,如分岔、混沌和从迭代中产生的分形。已知流的一维时间映射定义了一个离散动力系统,而一个离散动力系统是否能够嵌入连续动力系统则取决于其映射的迭代。在一维情况下,许多研究集中在具有有限个非单调点的非单调映射的整数或分数次迭代上。然而,对于具有无限个非单调点的情况,相关研究结果相对较少。本论文主要针对无限个非单调点的情况,研究了一类具有有限多平台的Markov平台映射,其平台均过对角线。首先通过单调性将此类平台映射分为四种情形,然后参考符号动力系统将平台端点迭代的原像点用序列与之对应,再分别给出了每种情形下所产的所有序列并将它们所对应的原像点进行排序,由此即可将区间分割并通研究在这些子区间的迭代给出了每种情形的任意整数次迭代的具体表达式。下图为文中DD情形下的具体迭代表达式:
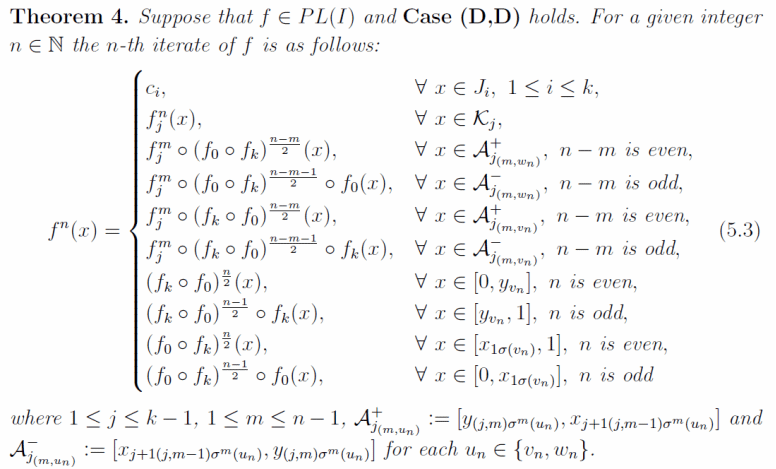
近年来,我校高度重视人才培养工作,狠抓人才质量,鼓励科学研究。我院紧紧围绕学校人才建设战略部署,发展特色的人才培养方式,为优秀青年提供广阔的发展平台与优渥资源,同时采取相关政策激励引导学院师生开拓创新。本次黄嘉驹最新研究成果成功被SCI三区期刊接收,既是对他研究成果的充分肯定,同时我院也将继续加强贯彻落实人才培养政策,为学校高质量发展贡献更多力量。
